Scan Compression
DFT Basics Article : #11

In my previous blog DFT Basics Article : #10, we explored scan chain reordering and how it helps avoid congestion.
In this blog, we will explore scan compression and how it helps in test time reduction and test data volume reduction.
Let’s get started !
Let us consider the following example to understand the need of scan compression.
Suppose there are 5,00,000 flops in the design
Case 1. There are 2 scan chains in the design
1 scan chain = 2,50,000 flops
Case 2. There are 50 scan chains in the design
1 scan chain = 10,000 flops
Case 3. There are 100 scan chains in the design
1 scan chain = 5000 flops
For which of the above 3 cases, Test time will be the least?
Test time = no. of patterns x no. of shift cycles per pattern x clock period of scan clock
For Case 3, Test time will be the least because the no. of flops per scan chain is the least. So the no. of shift cycles per pattern is less compared to other 2 cases.
This is an advantage of Case 3.
Disadvantage of Case 3
If we need 100 scan chains in our design, then we require 100 Sin and 100 Sout ports from top level.
But the no. of ports allocated for DFT will be limited.
Scan Compression
In order to overcome the disadvantage of case 3, we go for scan compression.
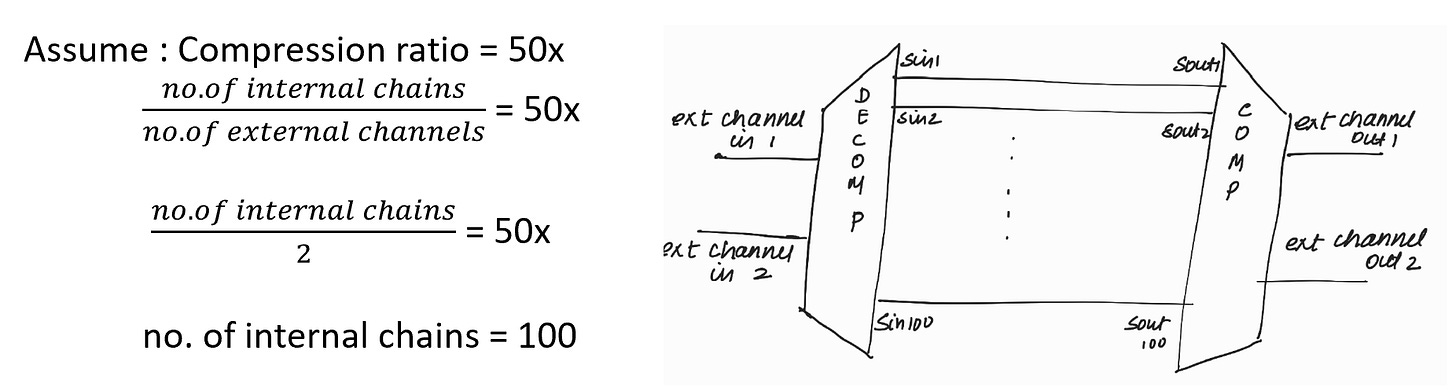
Internal chains (scan chains) will be compressed into external channels.
After going for scan compression, we require only 2 input and 2 output ports from the top level (in the above figure).
Therefore, we have overcome the disadvantage of Case 3.
Compression Ratio :
Example :
No. of external channels = 2
No. of internal chains = 100
Compression ratio = 100/2 = 50x
where x stands for how many times chains are compressed into channels.
Need of Scan Compression :
Reduction in Test Time
Reduction in Test Data Volume
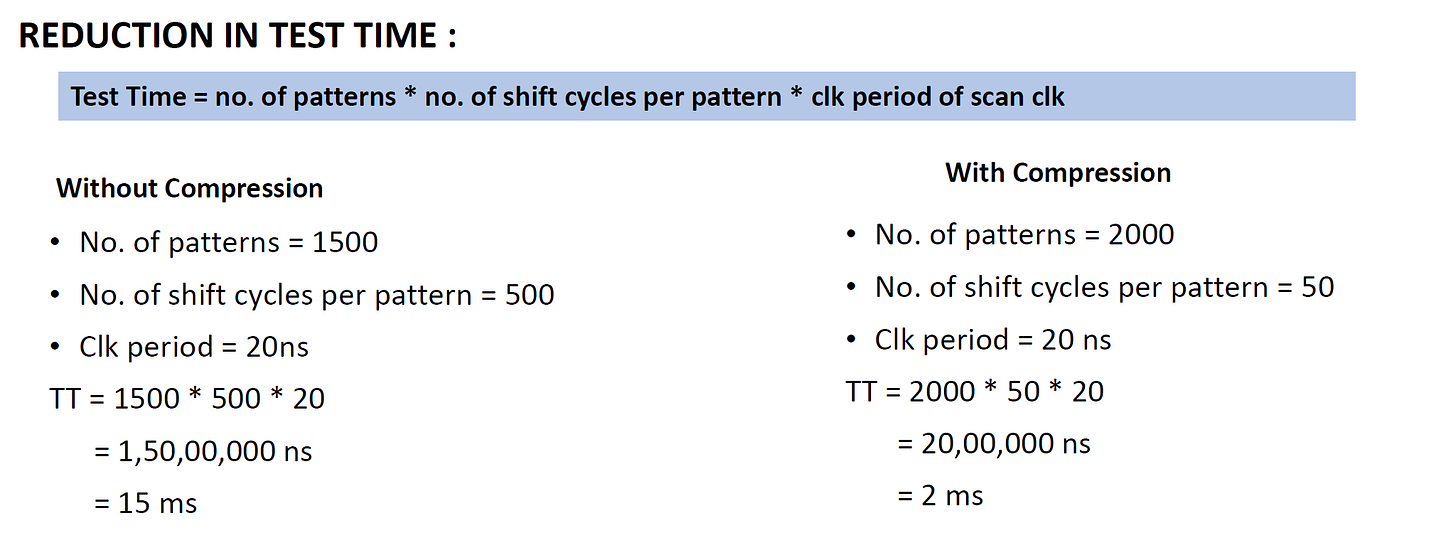
Reduction in Test Time :
Let us consider the following example to understand how compression helps in reduction of test time.
Suppose, there are :
5,00,000 flops in the design
4 top level ports allocated for DFT
Without Compression :
We can have only 2 scan chains.
=> 2,50,000 flops per scan chain
=> 2,50,000 shift cycles per pattern
since no. of shift cycles per pattern = no. of flops per scan chain. We have explored this in DFT Basics Article : #2
With Compression :
We can have 2 external channels
For example, if we have 100 internal chains
=> 5000 flops per scan chain
=> almost equal to 5000 shift cycles per pattern
After compression,
no. of shift cycles per pattern = no. of flops per chain + masking bits + initialization cycles
< < We will explore how we have arrived at this equation in the upcoming blogs >>
From the above example, we can see that, with compression, no. of shift cycles per pattern is less. So test time is less if we use compression.
So far, we have explored how compression helps reduce test time from a logical standpoint. Now, let us support this understanding with a formula-based approach.
< < Note : No. of patterns increases in compression (We will explore the reason during ATPG) > >
Reduction in Test Data Volume (no. of bits of pattern)
Let us consider the following example to understand how compression helps in reduction of test data volume.
Suppose, there are :
12 flops in the design
2 chains from top level
Without Compression :
With Compression :
< < We will explore about decompressor in detail in the next blog. > >
So far, we have explored how compression helps reduce test data volume from a logical standpoint. Now, let us support this understanding with a formula-based approach.
How to decide the no. of internal chains and external channels ?
Let us consider the following example to understand how to decide the no. of internal chains and external channels .
Assumption :
Total 1,00,000 flops are there in the design.
No. of top level ports allocated for DFT = 10 ports
Deciding the no. of external channels :
1. Allocate ports of mandatory DFT signals
• 2 Test clock - 2 ports
• Scan reset - 1 port
• SE - 1 port
• TM - 1 port
• EDT update - 1port
< < Note : TM will be controlled by JTAG. Just for illustration, it is considered that it is controlled from top level. > >
2. Subtract ports allocated for mandatory DFT signals from top level ports
10 – 6 = 4
3. With the remaining ports, decide the no. of external channels
1 external channel = 2 ports (1 input, 1 output)
For 4 ports, we can have 2 external channels
Deciding the no. of internal chains :
Let’s Assume that the compression ratio is 50x.
As calculated earlier, the number of external scan channels is 2
< < Note : Compression ratios usually don’t exceed 100x — we’ll dive into why that is in an upcoming blog. Usually compression ratios will be in the range of 80x > >
Deciding the scan chain length :
100 internal chains = 1,00,000 flops
=> 1 internal chain = 1000 flops